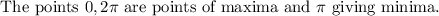Given:
The function f(x) = 3cos(x) - 2.
Required:
What are the minimum and maximum value of function?
Step-by-step explanation:
To check maximum and minimum value of function.
First derivate the original function.
After putting first derivative equal to zero, critical points can be found.
Then, do second deritvative to check points of maxima and minima.
The critical points at which second derivative greater than zero. Point will be of minima.
The critical points at which second derivative less than zero. Point will be of maxima.
So,
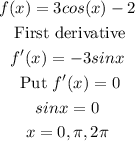
Now, do second derivative test for maximum and minimum points
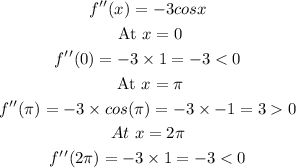
Answer: