Given the equation,
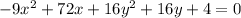
Complete squares as shown below,
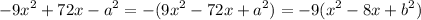
Thus,
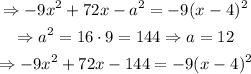
Similarly,
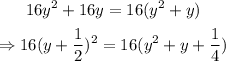
Therefore,
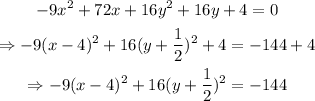
Finally, the standard form is.
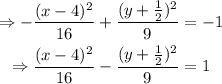
As for the vertices, foci, and asymptotes,
![\begin{gathered} c=\pm\sqrt[]{16+9}=\pm5 \\ \text{center:}(4,-(1)/(2)) \\ \Rightarrow\text{foci:}(4-5,-(1)/(2))_{},(4+5,-(1)/(2))_{} \\ \Rightarrow\text{foci:}(-1,-(1)/(2)),(9,-(1)/(2)) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/1rhu9g7hkz3afsu1vnydq39ycmyihayorw.png)
Foci: (-1,-1/2), (9,-1/2)
Vertices
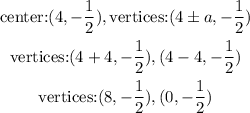
Vertices: (8,-1/2), (0,-1/2)
Asymptotes:
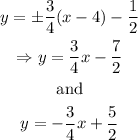
Asymptotes: y=3x/4-7/2 and y=-3x/4+5/2