Question

One evening 1400 concert tickets were sold for the Fairmont Summer Jazz Festival. Tickets cost $30 for covered pavilion seats and $20 for lawn seats. Total receipts were $32,000. Howmany tickets of each type were sold?How many pavilion seats were sold?

Answer 1

Let p be the number of pavilion seats and l be the number of lawn seats. Since there were sold 1400 tickets, we can write

`p+l=1400`

and since the total money was $32000, we can write

`30p+20l=32000`

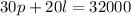
Then,we have the following system of equations

`\begin{gathered} p+l=1400 \\ 30p+20l=32000 \end{gathered}`

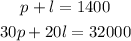
Solving by elimination method.

By multiplying the first equation by -30, we have an equivalent system of equation

`\begin{gathered} -30p-30l=-42000 \\ 30p+20l=32000 \end{gathered}`

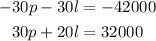
By adding these equations, we get

`-10l=-10000`

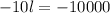
then, l is given by

`\begin{gathered} l=(-10000)/(-10) \\ l=1000 \end{gathered}`

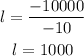
Now, we can substitute this result into the equation p+l=1400 and obtain

`p+1000=1400`

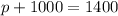
which gives

`\begin{gathered} p=1400-1000 \\ p=400 \end{gathered}`

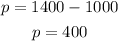
Then, How many tickets of each type were sold? 400 for pavilion seats and 1000 for lawn seats

How many pavilion seats were sold? 400 tickets