Question

Find all the solutions and if there is an extraneous solution, identify them and explain why they are extraneous.

Answer 1

Solution: b = 3

It is extraneous

Step-by-step explanation

We want to solve the equation given and to see if there are any extraneous solutions.

We have:

`\begin{gathered} \frac{7}{b\text{ + 3}}\text{ + }\frac{5}{b\text{ - 3}}\text{ = }\frac{10b}{b^2\text{ - 9}} \\ \Rightarrow\text{ }\frac{7}{b\text{ + 3}}\text{ + }\frac{5}{b\text{ - 3}}\text{ = }\frac{10b}{(b\text{ + 3)(b - 3)}} \\ \text{Multiply both sides by (b + 3)(b - 3):} \\ \Rightarrow\text{ }\frac{7(b+3)(b\text{ - 3)}}{b\text{ + 3}}\text{ + }\frac{5(b\text{ + 3)(b - 3)}}{b\text{ - 3}}\text{ = }\frac{10b(b\text{ + 3)(b - 3)}}{(b\text{ + 3)(b - 3)}} \\ 7(b\text{ - 3) + 5(b + 3) = 10b} \\ 7b\text{ - 21 + 5b + 15 = 10b} \\ \text{Collect like terms:} \\ 7b\text{ + 5b - 10b = 21 - 15} \\ 2b\text{ = 6} \\ Divide\text{ both sides by 2:} \\ b\text{ = }(6)/(2) \\ b\text{ = 3} \end{gathered}`

That is the solution to the equation.

To find if the solution is extraneous, we will insert the value of b = 3 into the original equation.

That is:

`\begin{gathered} \Rightarrow\text{ }\frac{7}{3\text{ + 3}}\text{ + }\frac{5}{3\text{ - 3}}\text{ = }\frac{10(3)}{(3\text{ + 3)(3 - 3)}} \\ (7)/(6)\text{ + }(5)/(0)\text{ = }(30)/((6)(0)) \\ (7)/(6)\text{ + }(5)/(0)\text{ = }(30)/(0) \end{gathered}`

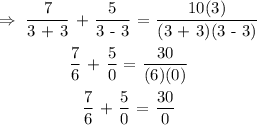
An extraneous solution is a solution that derives from solving a rational equation but does not exactly satisfy the original equation, that is, it is invalid for the equation.

By inserting b = 3 into the equation, we see that the equation is undefined.

Therefore, since b = 3 is a solution, but it does not satisfy the equation, it is an extraneous solution.