To find the quotient of the first part, we can start by noticing that all the factors on the denominator are present in all terms of the numerator, so we can factor those out and cancel with the denominator ones:
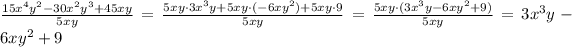
So, the first dropdown option is
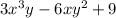
Also, this is the quotient, so we will use it for the second part.
The second part says that if we divide by one of the options (let's call it a), we will get:
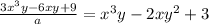
As we can see, no terms on the final result has fractional coefficient, so the number a has to be a common factor of all the terms coefficients. the coefficients are 3, -6 and 9, so the only common factors are 1 and 3, so the answer should be 3:

So, the second dropdown option is 3.