Answer:
Neither parallel nor perpendicular
Explanations:
The points are:
A(3, 1), B(3,-4), C(-4,1), D (-4,5)
The slope of a line is given as:
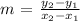
The slope of the line AB, m(AB), with gthe points A(3, 1), B(3,-4) is given as:

The slope of the line CD, m(CD), with the points C(-4,1), D (-4,5) is given as:
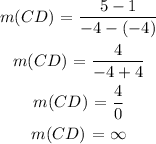
A line that has an infinite slope is a vertical line
For the two lines to be parallel, m(AB) should be equal to m(CD)
For the two lines to be perpendicular, m(AB) = -1 / m(CD)
None of the conditions for paralleleism and perpendicularity is met, the lines AB and CD are neither parallel nor perpendicular