Question

the 9th term of arithmetic sequence. Use the formula for 'an' to find 'a20', the 20th term of the sequence 7,3,-1,-5

Answer 1

We will find the value of the 20th term of the sequence 7, 3, -1, and -5.

We have the following sequence:

`7,3,-1,-5`

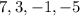
Finding the common difference

If we have an arithmetic sequence here, we need to find the common difference for this sequence, and we can do that by finding the difference between the second term and the first term, the difference between the third term and the second term, and so on. If we obtain the same value for the common difference, we have an arithmetic sequence here.

Then we have:

`\begin{gathered} d=3-7=-4 \\ \\ d=-1-3=-4 \\ \\ d=-5-(-1)=-5+1=-4 \end{gathered}`

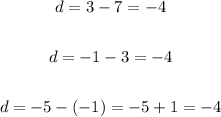
Then the common difference in this arithmetic sequence is d = -4.

Finding the formula for the arithmetic sequence

We know that the explicit formula for an arithmetic sequence is:

`a_n=a_1+(n-1)d`

For this case, we have that d = -4, and that the first term, a1 = 7. Then we have the formula for the arithmetic sequence:

`a_n=7+(n-1)(-4)`

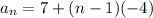
Notice that we can expand this expression as follows:

`\begin{gathered} a_n=7+(-4)(n)+(-4)(-1) \\ \\ a_n=7-4n+4 \\ \\ a_n=11-4n \\ \end{gathered}`

Finding the 20th term

Then to find the 20th term of the sequence, we have:

`\begin{gathered} a_(20)=7+(20-1)(-4) \\ \\ a_(20)=7+(19)(-4) \\ \\ a_(20)=7-76=-69 \\ \\ a_(20)=-69 \end{gathered}`

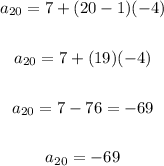
Therefore, in summary, we have that the value for the 20th term of the sequence 7, 3, -1, and -5 is -69.

,