Question

True or False? The end behaviors of each end of any quadratic function are always inthe same direction.

Answer 1

In general, given a quadratic function,

`\begin{gathered} f(x)=ax^2+bx+c \\ a,b,c\rightarrow\text{ constants} \end{gathered}`

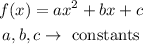
The end behaviors of each end of the function are given by the limits of f(x) when x approaches +/-infinite.

Therefore,

`\lim_(x\to\infty)f(x)=\lim_(x\to\infty)ax^2=a\lim_(x\to\infty)x^2=a*\infty`

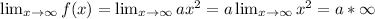
and

`\lim_(x\to-\infty)f(x)=\lim_(x\to-\infty)ax^2=a\lim_(x\to-\infty)x^2=a*\infty`

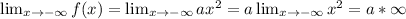
Thus, the two limits are the same and depend on the sign of a.

Hence, the answer is True, the statement is True.