The area of the trapezoid is changing at the rate of
 square inch per second at this moment. The correct answer is C) 1.
square inch per second at this moment. The correct answer is C) 1.
The area
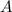 of a trapezoid can be found using the formula:
of a trapezoid can be found using the formula:
![\[ A = (1)/(2) * (a + b) * h \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/r62l3mqqs3dbb13d3nqrt9q3s5eupsiiek.png)
Given that the top base
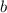 is increasing at the rate of
is increasing at the rate of
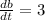 inches per second and the height
inches per second and the height
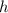 is decreasing at the rate of
is decreasing at the rate of
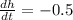 inches per second, we want to find the rate of change of the area
inches per second, we want to find the rate of change of the area
 at the moment when
at the moment when
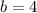 inches,
inches,
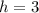 inches, and
inches, and
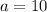 inches.
inches.
Differentiate the area formula with respect to time
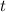 :
:
![\[ (dA)/(dt) = (1)/(2) * \left( (d)/(dt)(a + b) * h + (a + b) * (dh)/(dt) \right) \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/lgsvicy73icpkqrpn2gxywrwsf1n2n0sno.png)
Since
 is not changing,
is not changing,
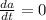 , and the formula simplifies to:
, and the formula simplifies to:
![\[ (dA)/(dt) = (1)/(2) * ( (db)/(dt) * h + (a + b) * (dh)/(dt)) \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/upmhqgthg07csydz5icfihe27x9e00wp7l.png)
Now we can plug in the given rates and values:
![\[ (dA)/(dt) = (1)/(2) * (3 * 3 + (10 + 4) * -0.5) \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/4xga7ikapcxwwspktliyv51y814jnku9yb.png)
![\[ (dA)/(dt) = (1)/(2) * (9 + 14 * -0.5) \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/r9rc2qumf179gqeknh5bbsxbx72g7e3y4n.png)
![\[ (dA)/(dt) = (1)/(2) * (9 - 7) \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/59zemk91ylopjop7huuylkqfgcw8tt1xzt.png)
![\[ (dA)/(dt) = (1)/(2) * 2 \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/fvtpv0l24gzyl6e0dm7385q581ugbe15ei.png)
![\[ (dA)/(dt) = 1 \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/5rni2mu9p2hhekmsieqldjqf352g2jsg3j.png)
Therefore, the area of the trapezoid is changing at the rate of
 square inch per second at this moment. The correct answer is C) 1.
square inch per second at this moment. The correct answer is C) 1.