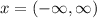Question

Solve quadratic equations -x^2 +3x < 3

Answer 1

The given quadratic inequation,

`-x^2+3x<3`

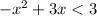
Subtract 3 on both sides,

`\begin{gathered} -x^2+3x-3<3-3 \\ -x^2+3x-3<0 \end{gathered}`

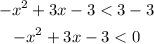
Multiply both sides by -1 that results in a change of symbol of the inequality,

`\begin{gathered} (-1)\cdot(-x^2+3x-3)>(-1)\cdot0 \\ x^2-3x+3>0 \end{gathered}`

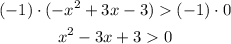
Use the method of completing squares,

`\begin{gathered} (x)^2-2(x)((3)/(2))+((3)/(2))^2-((3)/(2))^2+3>0 \\ (x-(3)/(2))^2-(9)/(4)+3>0 \\ (x-(3)/(2))^2+(3)/(4)>0 \\ (x-(3)/(2))^2^{}>-(3)/(4) \end{gathered}`

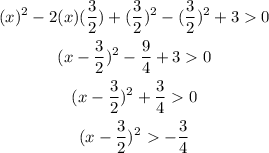
Consider that the square of any real number is always positive, and hence greater than a negative number.

So we can observe that the result obtained above is valid for all real number values of 'x'.

Thus, the solution of the given inequality is the set of all real numbers,

`x=(-\infty,\infty)`