Question

I only need the answer
THANK YOU!!

Answer 1

Answers:

`\cos(\theta) = (-3√(5))/(7)\\\\\tan(\theta) = -(2)/(3√(5)) = -(2√(5))/(15)\\\\\csc(\theta) = (7)/(2)\\\\\sec(\theta) = -(7)/(3√(5)) = -(7√(5))/(15)\\\\\cot(\theta) = (-3√(5))/(2)\\\\`

=================================================

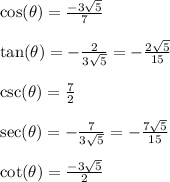
Step-by-step explanation:

We're given that
`\sin(\theta) = (2)/(7)\\\\`

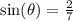
Plug that into the pythagorean trig identity
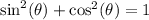`\sin^2(\theta)+\cos^2(\theta) = 1\\\\` and solve for cosine to find that
`\cos(\theta) = (-3√(5))/(7)\\\\`

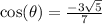
I skipped steps in solving so let me know if you need to see them.

Keep in mind that cosine is negative in quadrant 2

------------------

Once you've determined cosine, divide sine over cosine to get tangent

`\tan(\theta) = \sin(\theta) / \cos(\theta)\\\\\tan(\theta) = (2)/(7) / (-3√(5))/(7)\\\\\tan(\theta) = (2)/(7) * -(7)/(3√(5))\\\\\tan(\theta) = -(2*7)/(7*3√(5))\\\\\tan(\theta) = -(2)/(3√(5))\\\\\tan(\theta) = -(2√(5))/(3√(5)*√(5))\\\\\tan(\theta) = -(2√(5))/(3*5)\\\\\tan(\theta) = -(2√(5))/(15)\\\\`

------------------

To determine cosecant, we apply the reciprocal to sine.

`\sin(\theta) = (2)/(7) \to \csc(\theta) = (1)/(\sin(\theta)) = (7)/(2)\\\\`

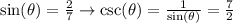
Similarly, secant is the reciprocal of cosine

`\cos(\theta) = (-3√(5))/(7) \to \sec(\theta) = (1)/(\cos(\theta)) = -(7)/(3√(5)) = -(7√(5))/(15)\\\\`

Depending on your teacher, rationalizing the denominator may be optional.

Lastly, cotangent is the reciprocal of tangent

`\tan(\theta) = -(2)/(3√(5))\to \cot(\theta) = (1)/(\tan(\theta)) = (-3√(5))/(2)`

------------------

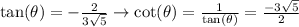
Side notes:

Sine and cosecant are the only things positive in Q2

Everything else (cosine, tangent, secant, cotangent) are negative in Q2.