Question

Which expression is equivalent to the quantity five raised to the negative second power times three raised to the fifth power end quantity all raised to the negative second power? three raised to the third power divided by five raised to the fourth power negative three raised to the third power divided by five raised to the fourth power five raised to the fourth power divided by three raised to the tenth power negative five raised to the fourth power divided by three raised to the tenth power

Answer 1

(c) five raised to the fourth power divided by three raised to the tenth power

Explanation:

You want the simplified version of the quantity five raised to the negative second power times three raised to the fifth power end quantity all raised to the negative second power.

Rules of exponents

The relevant rules of exponents are ...

(ab)^c = (a^c)(b^c)

a^-b = 1/a^b

(a^b)^c = a^(bc)

Application

The given expression can be simplified as follows:

`(5^(-2)3^5)^(-2)=5^((-2)(-2))3^((5)(-2))=5^43^(-10)=\boxed{(5^4)/(3^(10))}`

__

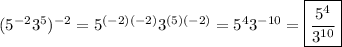
Additional comment

We find math expressions easier to understand when they are written using math notation, instead of words.