Question

Identify the graph that shows the feasible region for the following constraints.

X≥0
yzo
4x + 2y ≤ 40
2x + 4y ≤ 32

Answer 1

The feasible region is bounded by the corner points:

• (0, 0)
• (0, 8)
• (8, 4)
• (10, 0)

Explanation:

Given constraints:

`\begin{cases}x \geq 0\\y \geq 0\\4x+2y \leq 40\\2x+4y \leq 32\end{cases}`

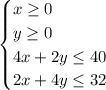
Rewrite the third and fourth inequalities to isolate y:

`\begin{aligned}\implies 4x+2y & \leq 40\\2y & \leq -4x+40\\y & \leq -2x+20\end{aligned}`

`\begin{aligned}\implies 2x+4y & \leq 32\\4y & \leq -2x+32\\y & \leq -(1)/(2)x+8\end{aligned}`

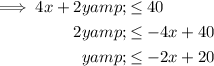
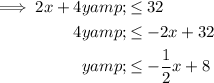
When graphing inequalities:

• < or > : dashed line.
• ≤ or ≥ : solid line.
• < or ≤ : shade under the line.
• > or ≥ : shade above the line.

Therefore:

• Draw the line x = 0 and shade above it (to the right).
• Draw the line y = 0 and shade above it.
• Draw the line y = -2x + 20 and shade below it.
• Draw the line y = -¹/₂x + 8 and shade below it.

The feasible region is the set of all possible values of the variables which satisfy the constraints.

Therefore, the feasible region is bounded by the corner points:

• (0, 0)
• (0, 8)
• (8, 4)
• (10, 0)