Question

Use the definition of a derivative to determine whether f(x) = 8x^2 is differentiable at x=0

Answer 1

The solution to determine whether
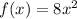`f(x) = 8x^2` is differentiable at x = 0: Yes, it is differentiable at x = 0. Option A is correct.

If the limit of the difference quotient exists and equals the slope of the function at that point, the function is differentiable at that location. The definition of the difference quotient is:

`f'(x) = lim_(h - > 0) (f(x + h) - f(x))/(h)`

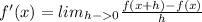
Let's evaluate the difference quotient for
`f(x) = 8x^2 at x = 0:`

`f'(0) = lim_(h - > 0) ((8(0+h)^2) - (8(0)^2))/(h)`

`f'(0) = lim_(h - > 0) (8h^2)/(h)`

`f'(0) = lim_(h - > 0) 8h`

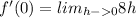
Given that the difference quotient's limit is equal to 0, we can infer that
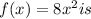`f(x) = 8x^2 is` differentiable at x = 0.