Question

Part 1. Create two radical equations: one that has an extraneous solution, and one that does not have an extraneous solution. Use the equation below as a model:a√x+b+c=dUse a constant in place of each variable a, b, c, and d. You can use positive and negative constants in your equation.Part 2. Show your work in solving the equation. Include the work to check your solution and show that your solution is extraneous.Part 3. Explain why the first equation has an extraneous solution and the second does not.

Answer 1

we have the equation

`a\sqrt[\square]{x+b}+c=d`

i will assume

a=2

b=5

c=3

d=5

solve for x

substitute the given values

`2\sqrt[\square]{x+5}+3=5`

subtract 3 both sides

`2\sqrt[\square]{x+5}=5-3`
`2\sqrt[\square]{x+5}=2`

Divide by 2 both sides

`\sqrt[\square]{x+5}=(2)/(2)`
`\sqrt[\square]{x+5}=1`

squared both sides

`\begin{gathered} x+5=\pm1 \\ x=-5\pm1 \end{gathered}`

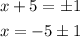
the values of x are

x=-4 and x=-6

Verify each solution

For x=-4

`\begin{gathered} \sqrt[\square]{-4+5}=1 \\ 1=1 \end{gathered}`

x=-4 ------> is a solution

Verify x=-6

`\begin{gathered} \sqrt[\square]{-6+5}=1 \\ \sqrt[\square]{-1}=1 \end{gathered}`

Is not true

therefore

x=-6 --------> is an extraneous solution