Question

15) A sample of 4 different calculators IS randomly selected from a group

containing 46 that are defective and 26 that have no defects. What is the
probability that all four of the
calculators selected are defective? Round to four
decimal places.
A) 0.1021
B) 0.1586
C) 0.1666
D) 10.9154

Answer 1

C) 0.1666

Explanation:

The probability of selecting a calculator that is defective can be defined as:
`(46)/(46+26)`

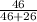
The 46 in the numerator is the number of calculators that are defective in the group. The 46 + 26 represents the total amount of calculators since 46 are defective and 26 are not defective and assuming a calculator can only be defective or not defective then these are the total number of calculators in the group.

This gives you a probability of approximately:
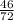`(46)/(72)` or approximately 0.638889

We can multiply independent events to find the combined probability of these events occurring. So we have to assume you put the calculator back into group after selecting one.

If this is the case we simply multiply 46/72 * 46/72 * 46/72 * 46/72 or (46/72)^4 to get an approximate probability of: 0.1666