Question

Consider the line y = -7x+7.

Find the equation of the line that is perpendicular to this line and passes through the point (4, 3).
Find the equation of the line that is parallel to this line and passes through the point (4, 3).
C
Equation of perpendicular line:
Equation of parallel line:

Answer 1

Answers:

Perpendicular Line:
`\text{y} = (1)/(7)\text{x}+(17)/(7)`

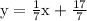
Parallel Line:
`\text{y} = -7\text{x}+31`

==================================================

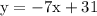
Step-by-step explanation:

The given equation is y = -7x+7 and it's in the form y = mx+b

• m = -7 = slope
• b = 7 = y intercept

Perpendicular lines will have a negative reciprocal slope, so we'll flip the fraction and the sign to go from -7 to 1/7 as the perpendicular slope.

The product of the original slope -7 and perpendicular slope 1/7 results in -1.

Let's now turn to point-slope form.

We'll plug in the perpendicular slope along with the coordinates of the point (4,3) to get the following result.

`\text{y} - \text{y}_1 = \text{m}(\text{x}-\text{x}_1)\\\\\text{y} - 3 = (1)/(7)(\text{x}-4)\\\\\text{y} - 3 = (1)/(7)\text{x}-(1)/(7)(4)\\\\\text{y} - 3 = (1)/(7)\text{x}-(4)/(7)\\\\`

`\text{y} = (1)/(7)\text{x}-(4)/(7)+3\\\\\text{y} = (1)/(7)\text{x}-(4)/(7)+(21)/(7)\\\\\text{y} = (1)/(7)\text{x}+(-4+21)/(7)\\\\\text{y} = (1)/(7)\text{x}+(17)/(7)\\\\`

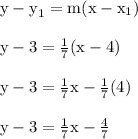
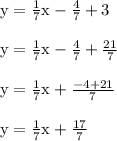
This is the equation of the perpendicular line that passes through (4,3)

-------------------------------------------

Parallel lines have equal slopes but different y intercepts.

Therefore, the slope of each line is m = -7

Once again we'll use point-slope form. The coordinates of (4,3) are used again, but we'll use a different m value compared to earlier.

`\text{y} - \text{y}_1 = \text{m}(\text{x}-\text{x}_1)\\\\\text{y} - 3 = -7(\text{x}-4)\\\\\text{y} - 3 = -7\text{x}+28\\\\\text{y} = -7\text{x}+28+3\\\\\text{y} = -7\text{x}+31\\\\`

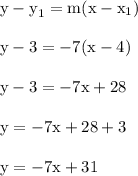
This is the equation of the parallel line passing through (4,3)