Substitute
 and
and
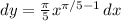 .
.
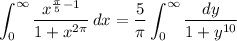
Now substitute
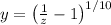 and
and
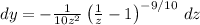 to get a beta integral.
to get a beta integral.
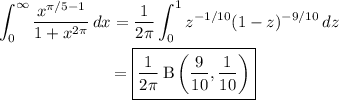
We can do better:
Recall that
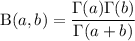
as well as the reflection formula for the gamma function,
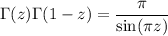
It follows that
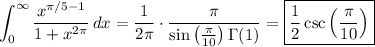
Even better:
To find an exact value for this result, recall
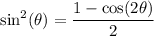
and
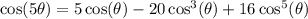
Then

Let
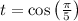 . Solve for
. Solve for
 in the quintic equation.
in the quintic equation.
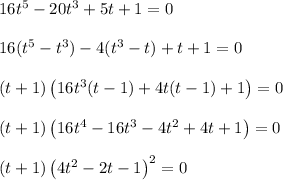
Clearly
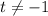 , so we're left with
, so we're left with

and
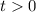 , so we take the positive root.
, so we take the positive root.
Now
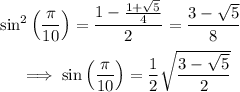
Denest the radical. Suppose there are rational
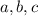 such that
such that

Squaring both sides gives
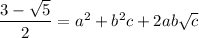
Let
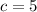 . Solve for
. Solve for
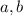 .
.
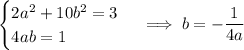
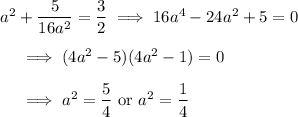
The first case leads to irrational
 , so we must have one of
, so we must have one of
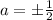 and
and
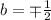 . The value of
. The value of
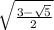 must be positive, which is consistent with
must be positive, which is consistent with
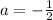 and
and
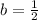 .
.
So we have
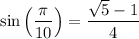
and the value of our integral is
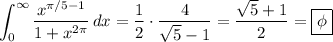
(i.e. the golden ratio)