Question

= a fx The function f is defined by f (x) = 50-3^x. The function g is defined by g(x) = a · Here are graphs of f and g. y مه f Х 1. How does a compare to 50? Explain how you know. 2. How does b compare to 3? Explain how you know. Edit View Insert Format Tools Table 12pt Paragraph В I U A o Tv :​

Answer 1

Explanation:

a, compares to 50 beacuse a means the staying point ; slope, so that’s why it starts at 50.

b, compares to 3 beacuse that is the y-intercept

Answer 2

1. The value of a is greater than 50 because the y-intercept of the exponential function g(x) is located above the y-intercept of f(x).

2. The value of b is less than 3 (but larger than 1) because the rate of growth of the exponential function f(x) is faster than the rate of growth of g(x).

In Mathematics and Geometry, an exponential function can be modeled by using this mathematical equation:

`f(x)=a(b)^x`

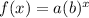
Where:

• a represents the initial value or y-intercept.
• x represents x-variable.
• b represents the rate of change or common ratio.

Part 1.

By critically observing the graph representing the two exponential functions f(x) and g(x), we can logically deduce that the value of a is greater than 50 because the y-intercept of the exponential function g(x) is located above the y-intercept of f(x).

Part 2.

Since the graph of g(x) lies below the graph of f(x), the value of b must be less than 3 (but larger than 1) because the rate of growth of the exponential function f(x) is faster than the rate of growth of g(x).

Complete Question:

The function f is defined by
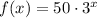`f(x) = 50 \cdot 3^x`. The function g is defined by
`g(x) = a \cdot b^x`.

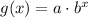Here are graphs of f and g.

1. How does a compare to 50? Explain how you know.

2. How does b compare to 3? Explain how you know.