First, we observe that
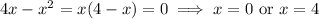
and

so that
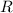 is in the first quadrant. Any line
is in the first quadrant. Any line
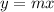 that slices this region into two pieces must then have a slope between
that slices this region into two pieces must then have a slope between
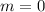 and
and
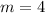 (which is the slope of the tangent line to the curve through the origin).
(which is the slope of the tangent line to the curve through the origin).
The parabola and line meet at the origin, and again when
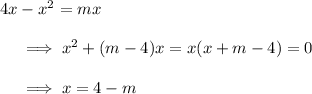
with
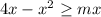 for
for
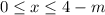 .
.
Now, the total area of
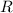 is
is
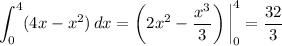
so that half the area is 16/3.
The area of the left piece (containing the origin) is
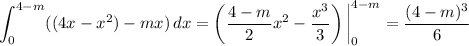
Solve for
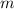 .
.
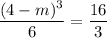
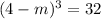
![4 - m = \sqrt[3]{32} = 2\sqrt[3]{4}](https://img.qammunity.org/2023/formulas/mathematics/college/q2ejprbaaa0kvxxpntjb7o4d1r6rhntx31.png)
![\boxed{m = 4 - 2\sqrt[3]{4} \approx 0.825}](https://img.qammunity.org/2023/formulas/mathematics/college/9drlirmrl99z27z9k9uh0srwsyja6dhr99.png)