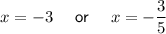Question

Solve the equation.

2|2x+3|=|x-3|
There should be two solutions.
Please show the steps and give an explanation on how to solve it and why.

Answer 1

x= -3

Explanation:

`2(2x + 3) = x - 3 \\ 4x + 6 = x - 3 \\ 4x = x - 3 - 6 \\ 4x - x = - 3 - 6 \\ 3x = - 9 \\ x = ( - 9)/(3) \\ x = - 3`

Answer 2

`x=-3 \textsf{ \quad or \quad} x=-(3)/(5)`

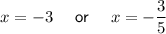
Explanation:

Given absolute value equation:

`2|2x+3|=|x-3|`

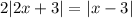
The absolute value of a number is its positive numerical value.

Therefore, the expressions inside the bars should be set to both positive and negative. Rewrite the absolute value equation as four equations without absolute value bars and simplify:

`\textsf{Positive = Positive}: \quad 2(2x+3)=x-3`

`\textsf{Positive = Negative}: \quad 2(2x+3)=-(x-3)`

`\begin{aligned}\textsf{Negative = Positive}: \quad -2(2x+3) &=x-3\\ \implies 2(2x+3) &=-(x-3)\end{aligned}`

`\begin{aligned}\textsf{Negative = Negative}: \quad -2(2x+3) &=-(x-3)\\ \implies 2(2x+3)&=x-3\end{aligned}`

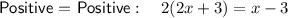
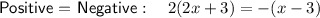
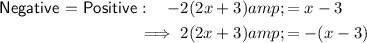
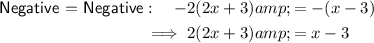
From inspection of the equations:

• Positive = Positive is equal to Negative = Negative, and
• Negative = Positive is equal to Positive = Negative,

so there are only two unique equations to be solved.

Equation 1

`\begin{aligned}2(2x+3) & =x-3\\4x+6 & = x-3\\4x+6-x&=x-3-x\\3x+6&=-3\\3x+6-6&=-3-6\\3x & =-9\\(3x)/(3) & = (-9)/(3)\\ x&=-3 \end{aligned}`

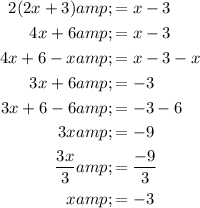
Equation 2

`\begin{aligned}2(2x+3)&=-(x-3)\\4x+6&=-x+3\\4x+6+x&=-x+3+x\\5x+6&=3\\5x+6-6&=3-6\\5x &=-3\\ (5x)/(5)&=(-3)/(5)\\x &=-(3)/(5) \end{aligned}`

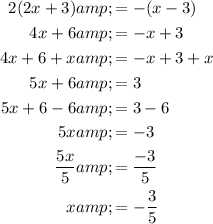
Therefore, the solutions are:

`x=-3 \textsf{ \quad or \quad} x=-(3)/(5)`