Answer:
Mean: 160
Median: 150
Mode: none
Range: 105
Standard deviation: 35.3
Explanation:
Given:
- Mean = 320
- Median = 300
- Mode = none
- Range = 210
- Standard deviation = 70.6
If each value in the data set is multiplied by a constant value, the mean, median, mode, range, and standard deviation will all be scaled by the same amount.
Therefore, if each value in the data set is multiplied by 0.5:
- Mean: 320 × 0.5 = 160
- Median: 300 × 0.5 = 150
- Mode: none × 0.5 = none
- Range: 210 × 0.5 = 105
- Standard deviation: 70.6 × 0.5 = 35.3
Proof
Data set: {1, 2, 3, 4, 5}
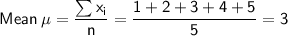



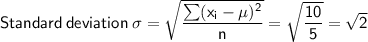
If we multiply each value by 0.5, the new data set is:
{0.5, 1, 1.5, 2, 2.5}
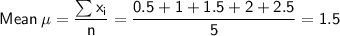


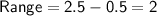
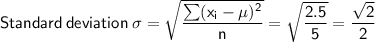
Therefore, if each value in the data set is multiplied by 0.5, the mean, median, mode, range, and standard deviation are all scaled by the same amount.