Answer:
0
Explanation:
Hi! We are given the limit expression:
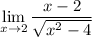
If we directly substitute x = 2 then we get 0/0 which is an indeterminate form. Therefore, we need to find other methods to evaluate the limit that does not become an indeterminate form.
As for rational function with square root in it, we conjugate the expression by multiplying both denominator and numerator with the square root expression.
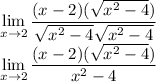
When two same square root expressions multiply each other, the square root is taken out as shown above.
From denominator, we can factor x²-4 to (x-2)(x+2) via differences of two squares.
Hence:
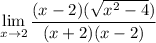
Cancel x-2.
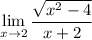
Then substitute x = 2 which we receive 0/4 = 0.
Henceforth, the limit value of expression is 0.