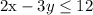Question

PLEAEE HELP FOR A BUNCH OF POINTS! i know the answer but i don’t know how to get to it! can someone please show me the work for this

the answer is 2x - 3y ≤ 12

Answer 1

Rise over run for the 2 (x) and 3 (y), Since the dot that’s obvious is (0,-4) then -4(-3) =12, which is why the 3 is negative

Answer 2

The points (0,-4) and (3,-2) are on the boundary line.

Find the slope

`(x_1,y_1) = (0,-4) \text{ and } (x_2,y_2) = (3,-2)\\\\m = (y_(2) - y_(1))/(x_(2) - x_(1))\\\\m = (-2 - (-4))/(3 - 0)\\\\m = (-2 + 4)/(3 - 0)\\\\m = (2)/(3)\\\\`

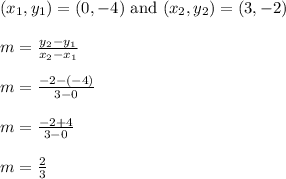
The y intercept is b = -4 since this is where the graph crosses the y axis.

Therefore,
`y = m\text{x} + b` will turn into
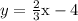`y = (2)/(3)\text{x} - 4` which is in slope intercept form.

--------------

From here, we convert to standard form Ax+By = C

Multiply both sides by the LCD 3 and then rearrange terms so that the x and y terms are on the same side

`y = (2)/(3)\text{x} - 4\\\\3y = 3\left((2)/(3)\text{x} - 4\right)\\\\3y = 3\left((2)/(3)\text{x}\right) + 3\left( - 4\right)\\\\`

`3y = 2\text{x} - 12\\\\3y+12 = 2\text{x}\\\\12 = 2\text{x}-3y\\\\2\text{x}-3y = 12\\\\`

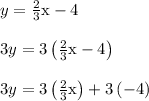
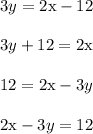
The equation of the boundary line, in standard form, is 2x-3y = 12

--------------

The last thing to do is to change the equal sign to one of the four inequality signs. The question is: which one?

Well we know there's an "or equal to" as part of the inequality sign due to the solid boundary line. If the boundary line were dotted or dashed, then we wouldn't have "or equal to".

So we'll go for either
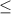`\le` or
`\ge`

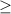
Let's try out a test point (0,0). This means we plug in x = 0 and y = 0

`2\text{x}-3y = 12\\\\2(0)-3(0) = 12\\\\0-0 = 12\\\\0 = 12\\\\`

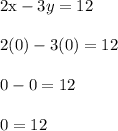
Clearly the last statement is false, but we can fix things by replacing each equal sign with a
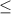`\le` sign

So,

`2\text{x}-3y \le 12\\\\2(0)-3(0) \le 12\\\\0-0 \le 12\\\\0 \le 12\\\\`

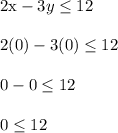
The last statement is true, which domino effects toward making the first statement true when (x,y) = (0,0). Note: if the boundary line went through the origin, then pick another point such as (0,1).

This effectively shows the shaded region involves the origin. Therefore we shade above the solid boundary line as shown in the given diagram.

This fully confirms why the answer is
`2\text{x}-3y \le 12`