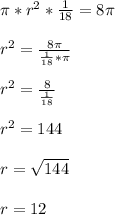Question

The area of a sector with angle 20 degrees is 8pi. What is the radius of the associated circle

Answer 1

R= 12.

Explanation:

First of all, let's sketch up this case to better understand what's going on. Check the attatched image below.

1. Finding a relative value.

How much is 20° or the whole circle?

Remember that a circle makes a total angle of 360°, therefore, 20°/360° is the percentage that this area of 8pi represent for this circle.

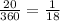`(20)/(360)= (1)/(18)` of the total circle.

Therefore, if we multiply the area A by this value of
`(1)/(18)`, we get the current value that we have, 8pi.

2. Constructing an equation.

Taking the information from step 1, the area of 8pi is given by the next expression:

`A*(1)/(18) =8\pi`

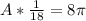
3. Rewrite the equation.

Remember that the formula for the area of a circle is the following:

`A=\pi r^(2)`

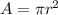
We can now substitute the equation of step 2 and write:

`\pi* r^(2)*(1)/(18) =8\pi`

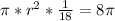
4. Solve the equation for r.

`\pi* r^(2)*(1)/(18) =8\pi\\\\r^(2)=(8\pi)/((1)/(18) *\pi ) \\\\r^(2)=(8)/((1)/(18) ) \\\\r^(2) =144\\\\r =√(144) \\\\r=12`