Question

A polynomial f (x) has the given zeros of 7, –1, and –3.

Part A: Using the Factor Theorem, determine the polynomial f (x) in expanded form. Show all necessary calculations. (3 points)

Part B: Divide the polynomial f (x) by (x2 – x – 2) to create a rational function g(x) in simplest factored form. Determine g(x) and find its slant asymptote. (4 points)

Part C: List all locations and types of discontinuities of the function g(x).
Ty<3

Answer 1

`\textsf{A)} \quad f(x) =x^3-3x^2-25x-21`

`\textsf{B)} \quad g(x)=((x-7)(x+3))/(x-2)`

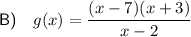
Slant asymptote: y = x - 2

C) Removable discontinuity at x = -1 ⇒ (-1, ¹⁶/₃)

Infinite discontinuity at x = 2

Explanation:

Factor Theorem

If f(x) is a polynomial, and f(a) = 0, then (x – a) is a factor of f(x).

Therefore, if the polynomial f(x) has the given zeros of 7, -1 and -3 then:

`f(x) = (x - 7)(x + 1)(x + 3)`

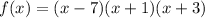
Expanded:

`\implies f(x) = (x - 7)(x + 1)(x + 3)`

`\implies f(x) = (x - 7)(x^2+4x+3)`

`\implies f(x) = x(x^2+4x+3) - 7(x^2+4x+3)`

`\implies f(x) =x^3+4x^2+3x - 7x^2-28x-21`

`\implies f(x) =x^3-3x^2-25x-21`

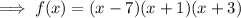
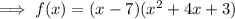
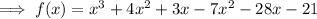
Part B

Factor
`x^2-x-2` :

`\implies x^2-2x+x-2`

`\implies x(x-2)+1(x-2)`

`\implies (x+1)(x-2)`

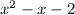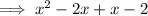
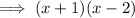
Therefore:

`\begin{aligned}\implies g(x) & = (f(x))/(x^2-x-2)\\\\ & = (x^3-3x^2-25x-21)/(x^2-x-2)\\\\& = ((x-7)(x+1)(x+3))/((x+1)(x-2))\\\\& = ((x-7)(x+3))/(x-2)\end{aligned}`

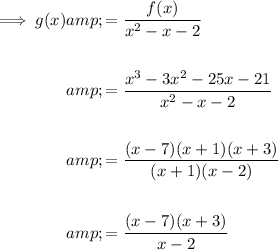
A slant asymptote occurs when the degree of the numerator polynomial is greater than the degree of the denominator polynomial.

To find the slant asymptote, divide the numerator by the denominator.

`\large \begin{array}{r}x-2\phantom{)}\\x-2{\overline{\smash{\big)}\,x^2-4x-21\phantom{)}}}\\\underline{-~\phantom{(}(x^2-2x)\phantom{-b)))}}\\0-2x-21\phantom{)}\\\underline{-~\phantom{()}(-2x+4)\phantom{)}}\\-25\phantom{)}\\\end{array}`

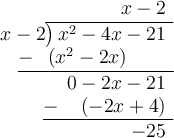
Therefore, the slant asymptote is y = x - 2.

Part C

Discontinuous function: A function that is not continuous.

Removable Discontinuity (holes): When a rational function has a factor with an x that is in both the numerator and the denominator.

Jump Discontinuity: The function jumps from one point to another along the curve of the function, often splitting the curve into two separate sections.

Infinite Discontinuity: When a function has a vertical asymptote (a line that the curve gets infinitely close to, but never touches).

Therefore, the discontinuities of function g(x) are:

• Removable discontinuity at x = -1 ⇒ (-1, ¹⁶/₃).

• Infinite discontinuity at x = 2.