Question

Line A passes through the points (-8, 5) and (-5, 4). Line B passes through the points (0, 1) and (4, -1). Which of the following describes the relationship between line A an line B?

1. Lines A and B are parallel, because they have opposite reciprocal slopes.
2. Lines A and B are parallel, because they have the same slope
3. Lines A and B intersect, because their slopes have no relationship.
4. Lines A and B are perpendicular, because they have opposite reciprocal slopes.

Answer 1

`\stackrel{\textit{\LARGE Line A}}{(\stackrel{x_1}{-8}~,~\stackrel{y_1}{5})\qquad (\stackrel{x_2}{-5}~,~\stackrel{y_2}{4})} ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{4}-\stackrel{y1}{5}}}{\underset{run} {\underset{x_2}{-5}-\underset{x_1}{(-8)}}} \implies \cfrac{4 -5}{-5 +8}\implies -\cfrac{1}{3} \\\\[-0.35em] ~\dotfill`

`\stackrel{\textit{\LARGE Line B}}{(\stackrel{x_1}{0}~,~\stackrel{y_1}{1})\qquad (\stackrel{x_2}{4}~,~\stackrel{y_2}{-1})} ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{-1}-\stackrel{y1}{1}}}{\underset{run} {\underset{x_2}{4}-\underset{x_1}{0}}} \implies \cfrac{-1 -1}{4 +0}\implies -\cfrac{1}{2}`

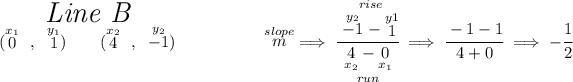
keeping in mind that perpendicular lines have negative reciprocal slopes, and that parallel lines have equal slopes, well, those two slopes above aren't either, so since they're neither, and they're different, that means that lines A and B intersect.