Question 6
1)
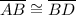 ,
,
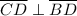 , O is the midpoint of
, O is the midpoint of
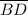 ,
,
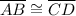 (given)
(given)
2)
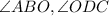 are right angles (perpendicular lines form right angles)
are right angles (perpendicular lines form right angles)
3)
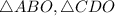 are right triangles (a triangle with a right angle is a right triangle)
are right triangles (a triangle with a right angle is a right triangle)
4)
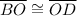 (a midpoint splits a segment into two congruent parts)
(a midpoint splits a segment into two congruent parts)
5)
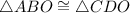 (LL)
(LL)
Question 7
1)
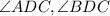 are right angles),
are right angles),
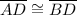
2)
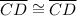 (reflexive property)
(reflexive property)
3)
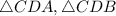 are right triangles (a triangle with a right angle is a right triangle)
are right triangles (a triangle with a right angle is a right triangle)
4)
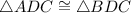 (LL)
(LL)
5)
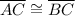 (CPCTC)
(CPCTC)
Question 8
1)
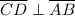 , point D bisects
, point D bisects
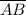 (given)
(given)
2)
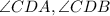 are right angles (perpendicular lines form right angles)
are right angles (perpendicular lines form right angles)
3)
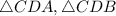 are right triangles (a triangle with a right angle is a right triangle)
are right triangles (a triangle with a right angle is a right triangle)
4)
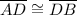 (definition of a bisector)
(definition of a bisector)
5)
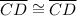 (reflexive property)
(reflexive property)
6)
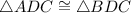 (LL)
(LL)
7)
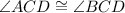 (CPCTC)
(CPCTC)