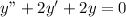Find a homogeneous linear differential equation with constant coefficients whose general solution is given by y=c1e−xcosx+c2e−xsinx.

Question

asked Jan 20, 2022 104k views

1 Answer

Bernd Wechner · Answer 1 · 2022-01-26T16:18:55+0000

Answer:

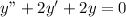
Explanation:

Given

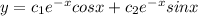
y=c_1e^(-x)cosx+c_2e^(-x)sinx

Required

Determine a homogeneous linear differential equation

Rewrite the expression as:

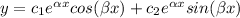
$y=c_1e^(\alpha x)cos(\beta x)+c_2e^(\alpha x)sin(\beta x)$

Where

$\alpha = -1$ and
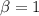
$\beta = 1$

For a homogeneous linear differential equation, the repeated value m is given as:

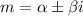
$m = \alpha \± \beta i$

Substitute values for
$\alpha$ and
$\beta$

$m = -1 \± 1*i$

$m = -1 \± i$

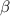
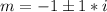
Add 1 to both sides

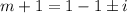
$m +1= 1 -1 \± i$

$m +1= \± i$

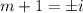
Square both sides

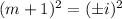
$(m +1)^2= (\± i)^2$

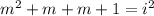
m^2 + m + m + 1 = i^2

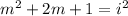
m^2 + 2m + 1 = i^2

In complex numbers:

i^2 = -1

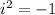
So, the expression becomes:

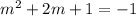
m^2 + 2m + 1 = -1

Add 1 to both sides

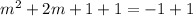
m^2 + 2m + 1 +1= -1+1

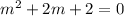
m^2 + 2m + 2= 0

This corresponds to the homogeneous linear differential equation