Answer:
169.04 in² (nearest hundredth)
Explanation:
Surface area of a cone =
 r² +
r² +
 r
r
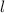
(where r = radius of the base and
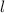 = slant height)
= slant height)
Given slant height
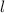 = 10 and surface area = 188.5
= 10 and surface area = 188.5
Surface area =
 r² +
r² +
 r
r
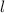
188.5 =
 r² + 10
r² + 10
 r
r
 r² + 10
r² + 10
 r - 188.5 = 0
r - 188.5 = 0
r =
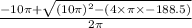 = 4.219621117...
= 4.219621117...
Volume of a cone = (1/3)
 r²h
r²h
(where r = radius of the base and h = height)
We need to find an expression for h in terms of
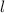 using Pythagoras' Theorem a² + b² = c², where a = radius, b = height and c = slant height
using Pythagoras' Theorem a² + b² = c², where a = radius, b = height and c = slant height
r² + h² =
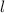 ²
²
h² =
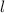 ² - r²
² - r²
h = √(
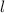 ² - r²)
² - r²)
Therefore, substituting found expression for h:
volume of a cone = (1/3)
 r²√(
r²√(
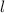 ² - r²)
² - r²)
Given slant height
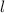 = 10 and r = 4.219621117...
= 10 and r = 4.219621117...
volume = 169.0431969... = 169.04 in² (nearest hundredth)