Question

An old mining tunnel disappears into a hillside. You would like to know how long the tunnel is, but it's too dangerous to go inside. Recalling your recent physics class, you decide to try setting up standing-wave resonances inside the tunnel. Using your subsonic amplifier and loudspeaker, you find resonances at 5.0 Hz and 6.4 Hz , and at no frequencies between these. It's rather chilly inside the tunnel, so you estimate the sound speed to be 333 m/s .

Answer 1

L = 116.6 m

Step-by-step explanation:

For this exercise we approximate the tunnel as a tube with one end open and the other closed, at the open end there is a belly and at the closed end a node, therefore the resonances occur at

λ = 4L 1st harmonic

λ = 4L / 3 third harmonic

λ = 4L / 5 fifth harmonic

General term

λ = 4L / n n = 1, 3, 5,... odd

n = (2n + 1) n are all integers

They indicate that two consecutive resonant frequencies were found, the speed of the wave is related to the wavelength and its frequency

v = λ f

λ = v / f

we substitute

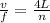
`(v)/(f) = (4L)/(n)`

L =
`n ( v)/(4f)`

for the first resonance n = n

L = (2n + 1)
`(v)/(4f_1)`

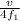
for the second resonance n = n + 1

L = (2n + 3)
`(v)/(4f_2)`

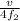
we have two equations with two unknowns, let's solve by equating

(2n + 1) \frac{v}{4f_1}= (2n + 3) \frac{v}{4f_2}

(2n + 1) f₂ = (2n +3) f₁

2n + 1 = (2n + 3)
`(f_1)/(f_2)`

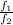
2n (1 - \frac{f_1}{f_2}) = 3 \frac{f_1}{f_2} -1

we substitute the values

2n (1-
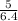`(5)/(6.4)`) = 3
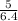`(5)/(6.4)` -1

2n 0.21875 = 1.34375

n = 1.34375 / 2 0.21875

n = 3

remember that n must be an integer.

We use one of the equations to find the length of the Tunal

L = (2n + 1) \frac{v}{4f_1}

L = (2 3 + 1)
`(333)/(4 \ 5.0)`

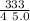
L = 116.55 m