Question

The total service time of a multistep manufacturing operation has a gamma distribution with mean 18 minutes and standard deviation 6 minutes.

(a) Determine the parameters alpha and lambda of the distribution. (solving these two parameters using the mean and the standard deviation)
(b) Assume that each step has the same exponential distribution for service time. What distribution for each step and how many steps produce this gamma distribution of total service time?

Answer 1

The answer is "
`\bold{r=9, \lambda=(1)/(2)\ and \ \ \text{exponential, 9 steps}}`"

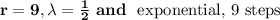Explanation:

In point a:

We are aware of the random gamma variable X:

`\to \mathbb{E} =(r)/(\lambda)\\\\\to Std(X) =(√(r))/(\lambda)\\\\`

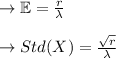
It is given:

`\to \mathbb{E} = 18 \\\\\to std(X)=6`

`\to 18=(r)/(\lambda)\\\\ \to 6=(√(r))/(\lambda)\\\\`

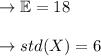
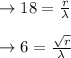
Substituting the value:

`\to (√(r))/(6)=(r)/(18)\\\\\to r=9\\\\\to \lambda=(1)/(2)\\\\`

In point b:

When building the Erlang/Gammas distribution, these could reasonably be assumed to become an exponential distribution only with \lambda = 1/2 parameter with one step but to be r = 9 for one step.