This question is incomplete, the complete question is;
The period of the leg can be approximated by treating the leg as a physical pendulum, with a period of 2π√[
 / mgh ] , where I is the moment of inertia, m is the mass, and h is the distance from the pivot point to the center of mass. The leg can be considered to be a right cylinder of constant density. For a man, the leg constitutes 16% of his total mass and 48% of his total height. Find the period of the leg of a man who is 1.85 m in height with a mass of 65 kg. The moment of inertia of a cylinder rotating about a perpendicular axis at one end is (m*
/ mgh ] , where I is the moment of inertia, m is the mass, and h is the distance from the pivot point to the center of mass. The leg can be considered to be a right cylinder of constant density. For a man, the leg constitutes 16% of his total mass and 48% of his total height. Find the period of the leg of a man who is 1.85 m in height with a mass of 65 kg. The moment of inertia of a cylinder rotating about a perpendicular axis at one end is (m*
 ^2)/3___________ sec.
^2)/3___________ sec.
Answer:
the period of the leg of the man is 1.5 sec
Step-by-step explanation:
Given the data in the question;
Time period = 2π√[
 / mgh ]
/ mgh ]
also, The moment of inertia of a cylinder rotating about a perpendicular axis at one end is ( m
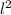 /3)
/3)
 = m
= m
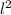 /3 and h =
/3 and h =
 /2
/2
hence;
Time period = 2π√[ m
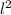 /3 / mgh ]
/3 / mgh ]
Time period = 2π√[ m
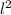 / 3mgh ]
/ 3mgh ]
Time period = 2π√[
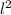 / 3g(
/ 3g(
 /2) ]
/2) ]
Time period = 2π√[ 2
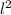 / 3g
/ 3g
 ]
]
Time period = 2π√[ 2
 / 3g ]
/ 3g ]
now,
 = 48% of 1.85 = 0.48 × 1.85 = 0.888 m
= 48% of 1.85 = 0.48 × 1.85 = 0.888 m
acceleration due to gravity g = 9.8 m/s²
so we substitute these values into the equation;
Time period = 2π√[ (2×0.888 ) / (3×9.8) ]
Time period = 2π√[ 1.776 / 29.8 ]
Time period = 2π√[ 0.059597 ]
Time period = 2π × 0.24412
Time period = 1.5 sec
Therefore, the period of the leg of the man is 1.5 sec