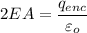Question

Use Gauss's Law to find the electric field produced by an infinite plane of uniformly distributed charge Q, with charge density σ. Draw the appropriate Gaussian Surface

Answer 1

Step-by-step explanation:

Consider an endless sheet of uniform charge thickness per unit area
`\sigma`

For a boundless sheet of charge, the electric field will be opposite to the surface. In this way, just the closures of a round and hollow Gaussian surface will add to the electric transition. For this situation, around and hollow Gaussian surface opposite to the charge sheet is utilized. The subsequent field is a large portion of that of a conductor at harmony with this surface charge thickness.

By balance, we expect the electric field on one or the other side of a plane to be an element of x just to be guided typical to the plane and to point away from/towards the plane contingent upon whether,
`\sigma` is positive/negative.

According to the law;

`2EA = (q_(enc))/(\varepsilon_o)`

`where; \ q_(enc) = total \ enclosed charge = \sigma A \\ \\ thus; \\ \\ 2EA = (\sigma A)/(\varepsilon_o) \\ \\ E = (\sigma)/(2 \varepsilon _o)`