Answer:
0.45 = 45% probability that the member uses the golf course but not the tennis courts
Explanation:
I am going to solve this question using the events as Venn sets.
I am going to say that:
Event A: Uses the golf courses.
Event B: Uses the tennis courts.
5% use neither of these facilities.
This means that
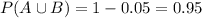
75% use the golf course, 50% use the tennis courts
This means, respectively, by:

Probability that a member uses both:
This is
 . We have that:
. We have that:
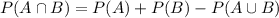
So
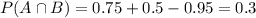
What is the probability that the member uses the golf course but not the tennis courts?
This is
 , which is given by:
, which is given by:
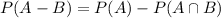
So
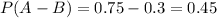
0.45 = 45% probability that the member uses the golf course but not the tennis courts