Solution :
For the reaction given :
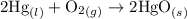
Thus we know that the equilibrium constant
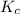 contains aqueous an dgas species only.
contains aqueous an dgas species only.
∴
![$K_c=(1)/([O_2])$](https://img.qammunity.org/2022/formulas/chemistry/college/jhrljhccg49vfib4pqdmaxgnpbvq0xv3ct.png) ............(1)
............(1)
Now at the equilibrium, an amount of the 13.4 g of oxygen was found in the vessel of 6.9 liters. For determining the concentration of the oxygen gas, we use :
![$[O_2]= (n_(O_2))/(V_(soln))$](https://img.qammunity.org/2022/formulas/chemistry/college/4qi38zej5mxrjcz7zx1403k7cqcfk13uox.png) ................... (2)
................... (2)
Here,
 = no. of moles of oxygen gas (mol)
= no. of moles of oxygen gas (mol)
 = volume of solution (L)
= volume of solution (L)
Therefore the number of moles of the oxygen gas is calculated by directly using the molecular weight (31.9988 g/mol) as the conversion factor.
∴
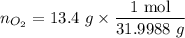
= 0.418 mol
Now substituting the known values in (2), we can find the equilibrium concentration of the oxygen gas :
![$[O_2] =\frac{0.418 \ \text{mol}}{6.9 \ \text{L}}$](https://img.qammunity.org/2022/formulas/chemistry/college/glawuxpmgo47kpsojgaon9jw9scofv0uwy.png)
= 0.0605 M
Therefore substituting the result in (1), the equilibrium constant for the reaction is :
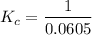
= 16.52