Question

)Suppose is a real number with 0 < < 4 . Set = sin( − ), = cos( + ), = sin( − ), and = cos(2 − ). Arrange the values , , , and in increasing order, and explain how you determined their order.

Answer 1

b < c < a < d

Explanation:

P.S - The exact question is -

Given - Suppose x is a real number with 0 < x <
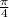`(\pi )/(4)` . Set a = sin(
`\pi` - x) ,

b = cos(
`\pi` + x) , c = sin( x -
`\pi`) , d = cos(2
`\pi` - x)

To find - Arrange the values of a, b, c, d in increasing order , and explain

how you determined their order.

Proof -

Firstly draw a unit circle where you indicate the following

A = ( cos(x), sin(x) )

B = ( cos(
`\pi` - x) , sin (
`\pi` - x) )

C = ( cos(
`\pi` + x), sin (
`\pi` + x) )

D = ( cos (2
`\pi` - x) , sin (2
`\pi` - x) )

As we have given that 0 < x <
`(\pi )/(4)`

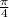
⇒sin (x) and cos(x) are positive and sin(x) < cos(x)

The figure is as follows :

Now

By seeing point B , we can say that

sin (
`\pi` - x) = sin (x) = a

By seeing point C , we can say that

cos(
`\pi` + x) = -cos (x) = b

By seeing point C , we can say that

sin( x -
`\pi`) = -sin(x) = c

By seeing point D , we can say that

cos(2
`\pi` - x) = cos(x) = d

As sin(x) < cos(x) ⇒ a < d

-sin(x) > -cos(x) ⇒ c > b ⇒ b< c

and as we know that -sin(x) < sin(x) ⇒ c < a

∴ we get

b < c < a < d