Question

Which ratio represents the cotangent of angle B in the right triangle below?

A. 5/3
B. 3/5
C. 3/4
D. 4/3

Answer 1

The cotangent of angle C is
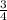`(3)/(4)`. So, the correct answer is option C:
`(3)/(4)`.

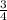In a right-angled triangle ABC, where angle B is the right angle, the cotangent of angle B is given by the ratio of the adjacent side to the opposite side. In this case, AC is the adjacent side, and CB is the opposite side.

Therefore, the cotangent of angle B is AC/CB.

Given that AC = x and CB = 12, the cotangent of angle B is x/12.

Now, we need to find the value of x. We can use the Pythagorean theorem, which states that in a right-angled triangle, the square of the length of the hypotenuse (AB in this case) is equal to the sum of the squares of the lengths of the other two sides. So,

`AB^2 =AC^2 +CB^2 .`

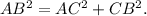
Substituting the given values, we get

`20^2 =x^2 +12^2.`

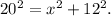
Solving for x:

`400=x^2 +144\\x^2 = 400 - 144= 256\\x= √(256) \\x= 16`

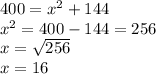
So, the cotangent of angle B is

`(12)/(16) = (3)/(4)`

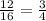
Therefore, the correct ratio representing the cotangent of angle B in the given triangle is C.
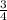`(3)/(4)`.

Answer 2

C. 3/4

Explanation:

Using the SOH CAH TOA identity;

tan theta = opposite/adjacent

From the diagram

Opposite = x

Adjacent = 12

tan <B = x/12

Since cot <B = 1/tan <B

cot <B = 12/x

Get x using pythagoras theorem

x² = 20²-12²

x² = 400 -144

x² = 256

x = 16

Hence cot <B = 12/16

cot <B =3/4