Question

A candy-filled piñata is hung from a tree for Elia's birthday. During an unsuccessful attempt to break the 4.4-kg piñata, Tonja smacks it with a 0.54-kg stick moving at 4.8 m/s. The stick stops and the piñata undergoes a gentle swinging motion. Determine the swing speed of the piñata immediately after being cracked by the stick

Answer 1

Answer: v = 0.6 m/s

Step-by-step explanation: Momentum Conservation Principle states that for a collision between two objects in an isolated system, the total momentum of the objects before the collision is equal to the total momentum of the objects after the collision.

Momentum is calculated as Q = m.v

For the piñata problem:

`Q_(i)=Q_(f)`

`m_(p)v_(p)_(i)+m_(s)v_(s)_(i)=m_(p)v_(p)_(f)+m_(s)v_(s)_(f)`

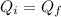
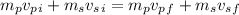
Before the collision, the piñata is not moving, so
`v_(p)_(i)=0`.

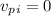After the collision, the stick stops, so
`v_(s)_(f)=0`.

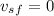Rearraging, we have:

`m_(s)v_(s)_(i)=m_(p)v_(p)_(f)`

`v_(p)_(f)=(m_(s)v_(s)_(i))/(m_(p))`

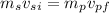
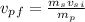
Substituting:

`v_(p)_(f)=((0.54)(4.8))/((4.4))`

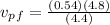
`v_(p)_(f)=` 0.6

Immediately after being cracked by the stick, the piñata has a swing speed of 0.6 m/s.