Question

The graph of a sinusoidal function has a maximum point at (0,5)(0,5)left parenthesis, 0, comma, 5, right parenthesis and then has a minimum point at (2\pi,-5)(2π,−5)left parenthesis, 2, pi, comma, minus, 5, right parenthesis. Write the formula of the function, where xxx is entered in radians.

Answer 1

f(x)=5sin((1/2)x + (pi/2))

Explanation:

Answer 2

The formula of the function is f(x)=5sin(x+π).

The general formula for a sinusoidal function is f(x)=asin(bx+c)+d, where a represents the amplitude, b represents the horizontal stretch, c represents the horizontal shift, and d represents the vertical shift.

In this case, we know that the amplitude is 5, since the maximum y-value is 5 and the minimum y-value is -5.

We also know that the midline is 0, since the maximum point is at (0,5) and the minimum point is at (2π,-5).

The horizontal stretch is
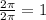`(2\pi)/(2\pi) =1` since the distance between the maximum point and the minimum point is 2π. The horizontal shift is
`(0 + 2\pi)/(2) = \pi`

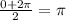
since the midpoint between the maximum point and the minimum point is π. Finally, the vertical shift is 0, since the midline is 0.

Therefore, the formula of the function is f(x)=5sin(x+π).