Question

Which of the following is a true statement regarding the slope? a. There is a positive association between calorie and carbohydrate content; however, because the slope is small the association between calories and carbohydrates is weak. b. A food item that has 100 calories above average is expected to have carbohydrates 1.1 grams over average. c. Because the lowest calorie content of food observed is 80, and 0.11 calories is well below this lowest value, this is extrapolation and cannot be trusted. d. All statements are true. e. None of the above statements are true.

Answer 1

Only option b is potentially correct as it describes a simple linear relationship based on the assumption of slope. However, without the numerical value of the slope or additional context, we cannot assess the accuracy or validity of the other statements, leading to the conclusion that the answer is e: None of the above statements are true.

Step-by-step explanation:

The question pertains to the analysis of slope and its implications on the relationship between caloric and carbohydrate content in food items. Of the given options, only statement b can be validated without additional information: A food item that has 100 calories above average is expected to have carbohydrates 1.1 grams over average. This statement assumes a simple linear relationship between calorie content and carbohydrate value represented by the slope. The caloric content approach using the Atwater system and the basic caloric contributions of fats, carbohydrates, and proteins are relevant in understanding the nutritional implications of these macronutrients.

Regarding statement a, without the numerical value of the slope, we cannot confirm the strength of the association, and statement c misrepresents the value 0.11 as a calorie measure instead of a slope, hence it's not valid. The nutritional value and calorie counts per gram of food components are crucial to determine the energy provided by different foods and understand how it affects diet and weight management. Therefore, the correct answer is e: None of the above statements are true.

Answer 2

The correct option is a.

The correct statement regarding the slope is that there is a positive association between calorie and carbohydrate content in Starbucks food items, as indicated by the positive slope of 0.11. However, the magnitude of the slope does not directly measure the strength of this association.

To evaluate the given statements about the slope of the regression line from the linear regression analysis, let's consider the regression equation provided:

`\[ \hat{y} = 8.94 + 0.11x \]`

where:

• 
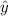  `\( \hat{y} \)` is the predicted amount of carbohydrates,
• 
  `\( x \)` is the number of calories,
• 8.94 is the y-intercept,
• 0.11 is the slope of the regression line.

The slope (0.11) indicates the amount of change in the predicted amount of carbohydrates for each one-unit change in calories.

Now, let's examine each statement:

a. Positive association: The slope is positive (0.11), which indicates that there is a positive association between calories and carbohydrates. However, the strength of the association is not solely determined by the magnitude of the slope but also by the variation explained by the regression model and the correlation coefficient. The statement is partially correct.

b. Calories above average: If a food item has 100 calories above average, the expected increase in carbohydrates can be calculated by multiplying the slope by 100. So, the expected increase in carbohydrates would be
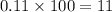`\( 0.11 * 100 = 11 \)` grams, not 1.1 grams. This statement is incorrect.

c. Extrapolation: The statement seems to misunderstand the slope. The slope of 0.11 does not represent calorie content; it represents the change in carbohydrate content per calorie. The statement about extrapolation is not applicable to the slope. This statement is incorrect.

d. All statements are true: Since at least one of the statements above is incorrect, this statement is also incorrect.

e. None of the above statements are true: Since statement a) is partially correct, this statement is not entirely true.

Therefore, based on the above analysis, the true statement regarding the slope is most closely related to statement a), with the caveat that it only indicates the direction of the association, not the strength. The other statements (b, c, d) are incorrect.

The complete question is here:

Image given below.

Options are:

a. There is a positive association between calorie and carbohydrate content; however, because the slope is small the association between calories and carbohydrates is weak.

b. A food item that has 100 calories above average is expected to have carbohydrates 1.1 grams over average.

c. Because a the lowest calorie content of food observed is 80, and 0.11 calories is well below this lowest value, this is extrapolation and cannot be trusted.

d. All statements are true.