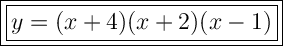Question

AYO 100 POINTS!!! Identify the equation for the graph! (polynomials)

Answer 1

B) y = (x + 4)(x + 2)(x - 1)

Explanation:

The graph shows a cubic function that crosses the x-axis at:

• 
  `x = -4`
• 
  `x = -2`
• 
  `x = 1`

The x-intercepts of a graph are the values of x that make the function equal to zero. According to the factor theorem, if f(c) = 0 then (x - c) is a factor of f(x). Therefore, the factors of the graphed function are:

`(x-(-4))=(x+4)`

`(x-(-2))=(x+2)`

`(x-1)`

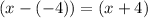
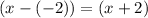
If a factor of a polynomial has an even exponent, it will touch the x-axis at the corresponding x-intercept and bounce off it without crossing the x-axis. Therefore, none of the factors have an even exponent.

If a factor of a polynomial has an exponent of 3, the curve at the corresponding x-intercept will exhibit an S-shaped behavior at the point where the curve intersects the x-axis. Therefore, none of the factors have an exponent of 3.

So, the equation for the graph is:

`\Large\boxed{\boxed{y=(x+4)(x+2)(x-1)}}`