Question

You may need to use the appropriate technology to answer this question. A sample of 27 items provided a sample mean of 29 and a sample standard deviation of 6 . Test the following hypotheses using a = 0.05 . What is your conclusion? H0​:σ2≤25H2​:σ2>25​ Find the value of the test statistic. Find the rho-value. (Round your answer to four decimal places.) p-value = What is your conclusion? Reject H0−​. We cannot conclude that the population variance is greater than 25 . Do not reject H0​. We can conclude that the population variance is greater than 25 . Reject H0​. We can conclude that the population variance is greater than 25 . Do not reject H0∗​. We cannot condude that the population variance is greater than 25 .

Answer 1

Using a significance level of 0.05, we perform a hypothesis test to determine whether the population variance is greater than 25. The test statistic is calculated to be 13.169 and the p-value is approximately 0.0681. Since the p-value is greater than the significance level, we do not have enough evidence to reject the null hypothesis.

Step-by-step explanation:

To determine whether we can conclude that the population variance is greater than 25, we need to perform a hypothesis test. Using a significance level of 0.05, we set up our hypotheses as follows:

H0: σ2 ≤ 25

H1: σ2 > 25

Next, we calculate the test statistic. Since the sample size is 27, we use a chi-square distribution with (n-1) degrees of freedom, which is 26 in this case. The test statistic is given by:

(n-1)s² / σ²

Plugging in the values, we get (27-1)(6²) / 25² = 13.169.

Now, we find the p-value associated with the test statistic. Since we have a right-tailed test, the p-value is the probability of observing a value greater than 13.169. Using the chi-square distribution with 26 degrees of freedom, we find that the p-value is approximately 0.0681.

Since the p-value (0.0681) is greater than the significance level (0.05), we do not have sufficient evidence to reject the null hypothesis. Therefore, we cannot conclude that the population variance is greater than 25.

Answer 2

The correct option is d.

The test statistic for the sample variance is 37.44. With a p-value of 0.0682, which is greater than the significance level of 0.05, we do not reject the null hypothesis. Therefore, we cannot conclude that the population variance is greater than 25.

To test the hypothesis for variance using the chi-squared distribution, we follow these steps:

1. State the null and alternative hypotheses:

`\( H_0: \sigma^2 = 25 \)`

`\( H_1: \sigma^2 > 25 \)`

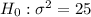
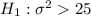
2. Calculate the test statistic using the formula:

`\( \chi^2 = ((n-1) \cdot s^2)/(\sigma^2_0) \)`

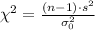
where
`\( n \)` is the sample size,
`\( s \)` is the sample standard deviation, and
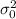`\( \sigma^2_0 \)` is the population variance under the null hypothesis.

For the given values:
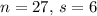`\( n = 27 \), \( s = 6 \)`, and
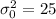`\( \sigma^2_0 = 25 \)`, the test statistic is:

`\( \chi^2 = ((27-1) \cdot 6^2)/(25) = 37.44 \)`

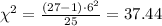
3. Determine the p-value:

The p-value is the probability of obtaining test results at least as extreme as the results actually observed, under the assumption that the null hypothesis is correct. For a chi-squared test with
`\( \chi^2 = 37.44 \)` and
`\( df = n-1 = 26 \)`, the p-value is:

`\( p = 1 - \text{CDF}(37.44) = 0.0682 \)`

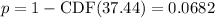
4. Compare the p-value with the significance level
`\( \alpha = 0.05 \)`:

Since the p-value
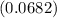`\( (0.0682) \)` is greater than
`\( \alpha \)`, we do not have sufficient evidence to reject the null hypothesis.

5. Conclusion:

Based on the computed p-value, we do not reject
`\( H_0 \)`. We cannot conclude that the population variance is greater than 25.

The complete question is here: