Answer:
P(x = 7) = 0.0138 (4 d.p.)
Explanation:
To find the probability that exactly 7 out of 15 Southwest flights arrive late when the on-time rate is 80%, we can use the binomial probability formula:
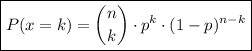
where:
- n is the number of trials.
- k is the number of successful trials.
- p is the probability of success.
In this case:
- The number of trials is the number of flights, so n = 15.
- The successful trials are the number of flights arriving late, so k = 7.
- The probability of "success" is the probability of a flight arriving late, so p = 1 - 0.80 = 0.2.
Calculate the probability by substitute the values into the formula:

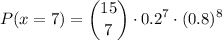


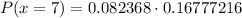
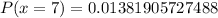
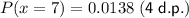
Therefore, the probability that exactly 7 out of 15 Southwest flights arrive late is approximately 0.0138 (rounded to four decimal places).