Question

During take off, a plane leaves the ground and travels in a straight line until it reaches a height of 11 km. The distance the plane flies during take off should be in the range 65 km to 69 km.

What is the smallest possible angle that the path of the plane could make with the ground?

Answer 1

Explanation:

Consider a right-angled triangle. We have 11/69 ≤ sin(theta) ≤ 11/65.

Since we're interested in the minimum, we have theta = arcsin(11/69) ≈ 0.160 rad.

Answer 2

9.17°

Explanation:

The given scenario can be modeled as a right triangle, where the height of the triangle is 11 km, and the path of the plane is the triangle's hypotenuse.

The smallest possible angle that the path of the plane could make with the ground occurs when the hypotenuse is the longest possible length, which is 69 km.

To find the angle, we can use the sine ratio:

`\boxed{\begin{array}{l}\underline{\textsf{Sine trigonometric ratio}}\\\\\sf \sin(\theta)=(O)/(H)\\\\\textsf{where:}\\\phantom{ww}\bullet\;\textsf{$\theta$ is the angle.}\\\phantom{ww}\bullet\;\textsf{O is the side opposite the angle.}\\\phantom{ww}\bullet\;\textsf{H is the hypotenuse (the side opposite the right angle).}\end{array}}`

In this case:

• O = 11 km
• H = 69 km

Substitute these values into the sine ratio and solve for angle θ:

`\sin \theta=(11)/(69)`

`\theta=\sin^(-1)\left((11)/(69)\right)`

`\theta=9.17324938...^(\circ)`

`\theta=9.17^(\circ)\; \sf (2\;d.p.)`

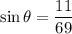
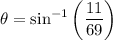
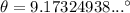
Therefore, the smallest possible angle that the path of the plane could make with the ground is approximately 9.17° when it travels a distance of 69 km during take-off.