Question

a 1.50 kg granite stone is tied to a rope and spun in a circular path of radius 1.08 m. the stone obtains a maximum speed of 12.0 m/s. what is the magnitude of the maximum radial acceleration (in m/s2) of the stone?

Answer 1

Approximately
`133\; {\rm m\cdot s^(-2)}`.

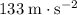Step-by-step explanation:

When an object moves along a circular path, the acceleration of the object will point to the center of the path. This acceleration is referred to as centripetal acceleration (also known as radial acceleration.) The magnitude of this acceleration is proportional to the square of the speed of the motion:

`\displaystyle a = (v^(2))/(r)`,

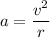Where:

• 
  `a` is the magnitude of the centripetal (radial) acceleration,
• 
  `v` is the speed of the motion, and
• 
  `r` is the radius of the circular path.

Given that
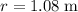`r = 1.08\; {\rm m}`, substitute in the maximum value of speed
`v` to find the maximum magnitude of acceleration:

`\begin{aligned}a &= (v^(2))/(r) \\ &= ((12)^(2))/(1.08)\; {\rm m\cdot s^(-2)} \\ &\approx 133\; {\rm m\cdot s^(-2)}\end{aligned}`.

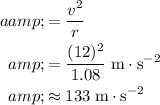In other words, the maximum radial acceleration of this object would be approximately
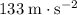`133\; {\rm m\cdot s^(-2)}`.