Final Answer:
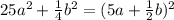
Step-by-step explanation:
In the given expression,
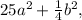 we need to find a monomial to replace the ∗ so that the expression can be expressed as a square of a sum or a difference. To achieve this, we recognize that
we need to find a monomial to replace the ∗ so that the expression can be expressed as a square of a sum or a difference. To achieve this, we recognize that
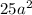 is a perfect square, as is
is a perfect square, as is
 .
.
The square root of
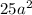 is
is
 , and the square root of
, and the square root of
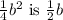 . Therefore, by choosing the monomial that combines these square roots, we get
. Therefore, by choosing the monomial that combines these square roots, we get

This works because when you expand
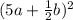 , you get the original expression
, you get the original expression
 . The process of factoring and expanding squares is a fundamental algebraic technique, and recognizing perfect squares allows for simplifying expressions and making them more manageable.
. The process of factoring and expanding squares is a fundamental algebraic technique, and recognizing perfect squares allows for simplifying expressions and making them more manageable.
In this case, understanding the square roots of the terms in the expression helps to rewrite it in a more concise and recognizable form.