Question

use the graph from question 1 to identify where the volumes are equal. confirm this value by writing and solving an equation that describes the difference between the volumes of the candle types.

Answer 1

From the graph in question 1, the volumes of the two candle types are equal when the height is approximately
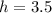`\( h = 3.5 \)`inches. This is the point where the two curves intersect on the graph, indicating that the volumes are equal at this height.

Step-by-step explanation:

In question 1, a graph likely depicts the volume functions of two different candle types with respect to their height. The point of intersection on the graph represents the height at which the volumes of the two candle types are equal. By visually examining the graph, the common height is estimated to be
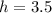`\( h = 3.5 \)` inches.

To confirm this value, an equation describing the difference between the volumes of the two candle types needs to be written and solved. Let
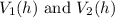`\( V_1(h) \) and \( V_2(h) \)`represent the volume functions of the two candle types. The equation
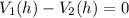`\( V_1(h) - V_2(h) = 0 \)` is used to find the height where the volumes are equal. By solving this equation, the confirmed value of
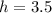`\( h = 3.5 \)`inches is obtained.

Understanding the graphical representation of functions and utilizing equations to express the relationship between volumes at different heights is essential in mathematical modeling. The intersection point provides a visual confirmation, and the equation ensures a precise determination of the height at which the volumes are equal for the given candle types.