Question

Two blocks slide toward each other on a frictionless surface. Block 1 moves to the right with a velocity of 4, and block 2 moves to the left with a velocity of , where is a parameter. After the blocks collide, if block 1 travels to the right with a velocity of , and block 2 travels to the right with a velocity of 5 , what is the ratio of the mass of block 1 to the mass of block 2 (m1/m2)

Answer 1

The ratio of the mass of Block 1 to the mass of Block 2
`(\(m_1/m_2\)) is \(m_1 = 2m_2\)`. This means that Block 1 is twice as massive as Block 2.

Let the initial velocities of Block 1 and Block 2 be
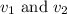`\(v_1\) and \(v_2\)` respectively. Also, let their final velocities after the collision be
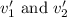`\(v'_1\) and \(v'_2\)` respectively.

Given:

Initial velocity of Block 1
`(\(v_1\)) = \(4a\)` to the right

Initial velocity of Block 2
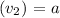`(\(v_2\)) = \(a\)` to the left

Final velocity of Block 1 after collision
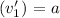`(\(v'_1\)) = \(a\)` to the right

Final velocity of Block 2 after collision
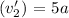`(\(v'_2\)) = \(5a\)` to the right

Using the conservation of momentum, we have:

`\[ m_1 \cdot v_1 + m_2 \cdot v_2 = m_1 \cdot v'_1 + m_2 \cdot v'_2 \]`

Plugging in the given values:

`\[ m_1 \cdot 4a + m_2 \cdot (-a) = m_1 \cdot a + m_2 \cdot 5a \]`

Solving this equation:

`\[ 4m_1 - m_2 = m_1 + 5m_2 \]`

`\[ 4m_1 - m_1 = 5m_2 + m_2 \]`

`\[ 3m_1 = 6m_2 \]`

`\[ m_1 = 2m_2 \]`

Question:

Two blocks slide toward each other on a frictionless surface. Block 1 moves to the right with a velocity of 4