Question

(b) Find the matrix, rank, and nullity of the transformation: T:P3(R)→P3(R) defined by T(f(x))=f′(x)+2f′′(x)+∫0x50f(t)dt, where f′ and f′′ are first derivative and second derivative of f respectively

Answer 1

`\sf{\blue{«} \: \pink{ \large{ \underline{A\orange{N} \red{S} \green{W} \purple{E} \pink{{R}}}}}}`

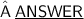
Certainly! The transformation
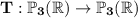`\bf\:T: \mathbb{P}_3(\mathbb{R}) \rightarrow \mathbb{P}_3(\mathbb{R})` defined by

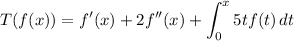
`\displaystyle\:T(f(x)) = f'(x) + 2f''(x) + \int_0^x 5t f(t) \, dt`

in
`\bf\:\mathbb{P}_3(\mathbb{R})`, where
`\bf\:f'` and
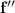`\bf\:f''` are the first and second derivatives of
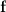`\bf\:f` respectively.

To find the matrix representation of this transformation, we can represent the derivatives and the integral as linear transformations and then construct the matrix. The transformation matrix
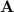`\bf\:A` for
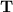`\bf\:T` can be found by evaluating
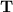`\bf\:T` on the standard basis
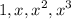`\displaystyle\:1, x, x^2, x^3` of
`\displaystyle\:\mathbb{P}_3(\mathbb{R})`.

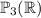After evaluating, the matrix
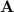`\bf\:A` would be:

`A = \begin{bmatrix}0 & 1 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 5/2 \\ 0 & 0 & 0 & 0\end{bmatrix}`

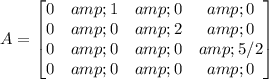
The rank of the matrix
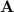`\bf\:A` is 3, and the nullity is 1.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`